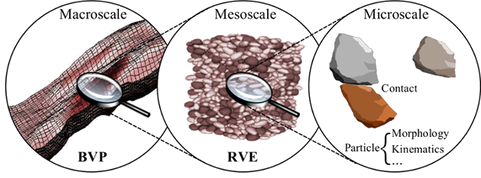
Hierarchical Multiscale Approach (HMA)
|
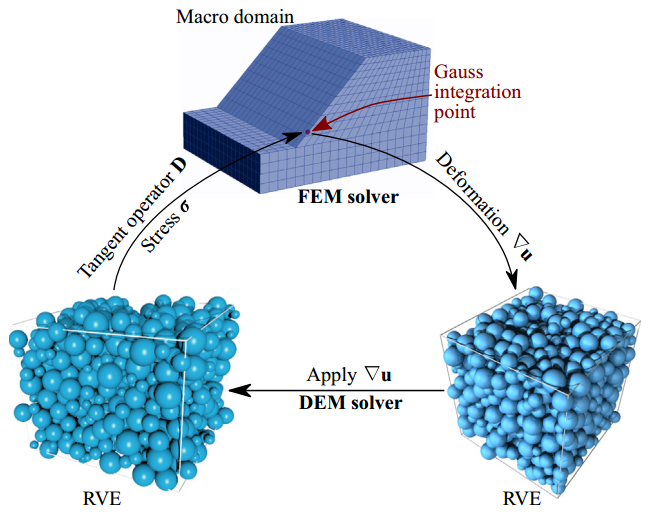
This fact motivates the development of HMA: FEM is used to discretize the large-scale physical domain and to solve the boundary value problem (BVP). Each Gauss integration point of the FE mesh is attached with a representative volume element (RVE) which is solved by DEM simulations. The local boundary condition for DEM is obtained from FEM solution; stress and tangent modulus are then homogenized from the RVE packing and passed to FEM for updated solution. HMA offers two major advantages: first, it bypasses the assumption of phenomenological constitutive law; second, it facilitates macro-micro bridging in analyzing granular media behaviors.
|
|
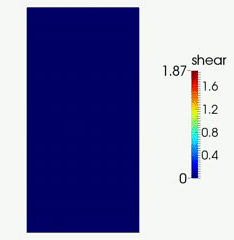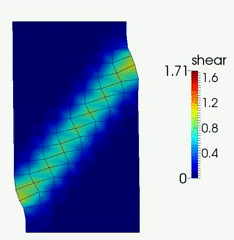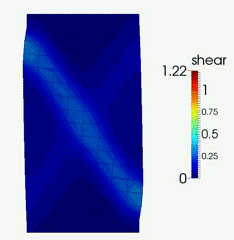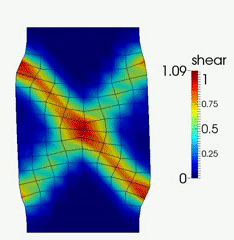
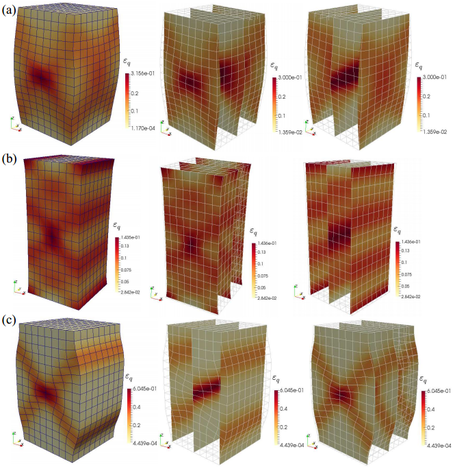
HMA has been successfully applied to simulate strain localization in granular soils subjected to general three-dimensional loading conditions, including (a) conventional triaxial compression (CTC); (b) conventional triaxial extension (CTE) and (c) plane-strain biaxial compression (PBC). Complex shear band patterns were observed: 3D octopus-shaped localization zone in CTC; multiple conjugate planar shear bands in CTE; and single pair conjugate planar shear bands in PBC.
To explore the detail of HMA and its application in analyzing strain localization in granular soils, please refer to Guo & Zhao (2014, IJNME), Zhao & Guo (2015, Géotechnique) and Guo & Zhao (2016, CG).
|
HMA with Applications in Geotechnical Engineering
|
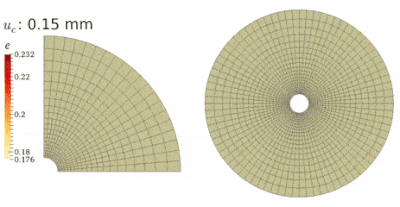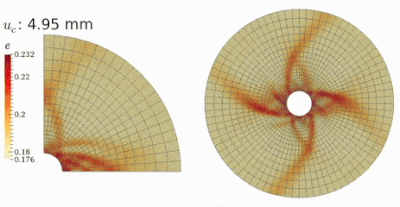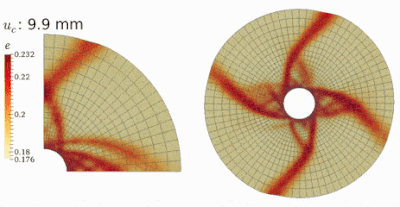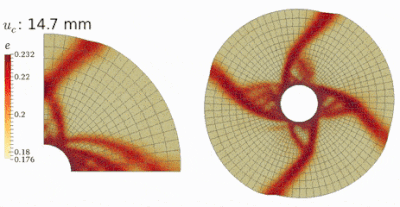
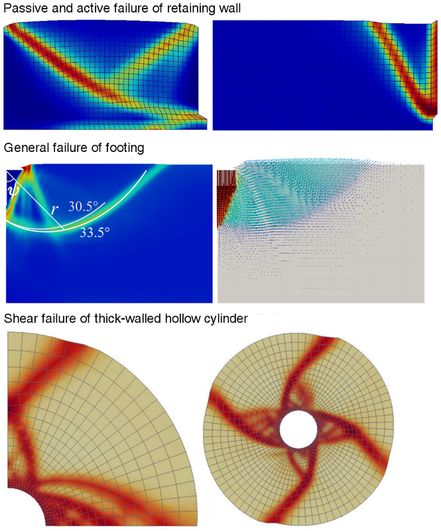
More complex BVPs have been investigated by HMA. The first figure shows the passive and the active failure modes of a rough retaining wall under the translational mode. The second figure shows the general failure of a shallow foundation (footing). A downward inverse triangle and a spiral curve are observed, which cause excessive settling beneath the footing and large heaving beside the footing. The third figure shows the shear failure of a thick-walled hollow cylinder simulated by simplified quarter-domain and complete full-domain models. Curvilinear shear zones have been observed in both tests which emanate from the inner surface and propagate toward the exterior surface.
Please refer to Guo & Zhao (2015, IJNAMG) and Guo et al. (2016, GL) for more information on the applications of HMA in geotechnical engineering.
|
HMA in Solving Coupled Hydro-Mechanical Problems
|
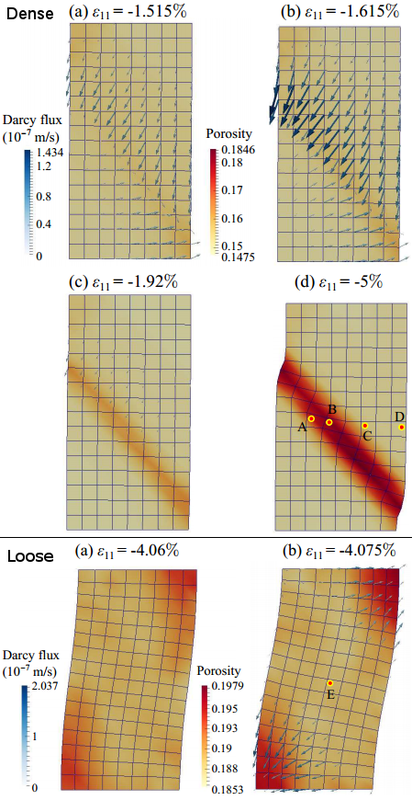
To enrich the predictive capacity of HMA for simulating saturated granular soils, a coupled u-p formulation is proposed which considers the effects of pore water pressure in the macroscale and invokes the Terzaghi's effective stress principle to obtain the effective stress from microscale DEM computations. The total stress is then superimposed from the effective stress homogenized from mesoscale RVE packings and the pore water pressure. To solve the coupled governing equations at the macroscale, an operator-split method (fixed-stress split) is employed. The overall methodology is proved viable and economic compared with expensive microscopic fluid-particle coupling approach, and has been applied to model 1D/2D consolidation problems and globally undrained biaxial compression tests on both dense and loose samples. The right figures show the contours of void ratio and Darcy flow patterns, indicating of strain localization and diffuse liquefaction, for dense and loose samples respectively. The dilative shear band in the dense sample leads to an increase of permeability inside the localized zone. Hence, an into-band flow pattern is observed. Please refer to Guo & Zhao (2016, CMAME) for more details.
|
Micromechanics and Physics of Granular Media
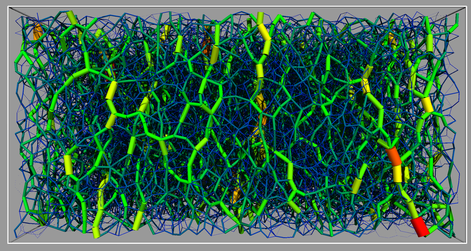
Top-left: force-chains for a sheared granular system at the critical state indicating strong anisotropy;
Top-right: contact normal distribution before and after shearing showing isotropic and anisotropic fabrics;
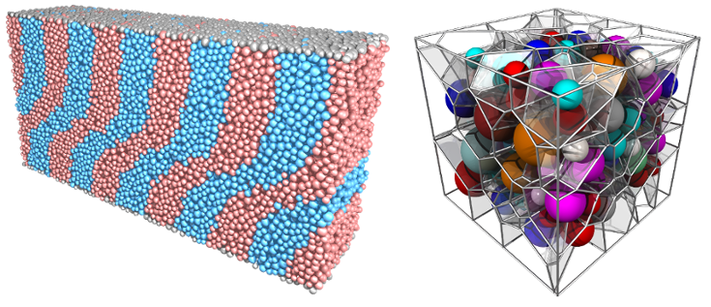
Bottom-left: shear banding in a granular system subjected to Couette shear;
Bottom-right: Voronoi tessellation for a diffuse granular packing.
Please refer to Guo & Zhao (2013, CG), Zhao & Guo (2013, Géotechnique), Zhao & Guo (2014, AMSS), and Guo & Zhao (2014, PRE) for the intriguing phenomena in granular materials.
Top-right: contact normal distribution before and after shearing showing isotropic and anisotropic fabrics;
Bottom-left: shear banding in a granular system subjected to Couette shear;
Bottom-right: Voronoi tessellation for a diffuse granular packing.
Please refer to Guo & Zhao (2013, CG), Zhao & Guo (2013, Géotechnique), Zhao & Guo (2014, AMSS), and Guo & Zhao (2014, PRE) for the intriguing phenomena in granular materials.